Page 8 - base

“Uncertainty-noise” Le Mans7
Acoustique
&
Techniques n° 40
In the GUM supplement 1 it is proposed to propagate
distribution instead of the propagation of variance as it is
described in the GUM procedure of chapter 8.
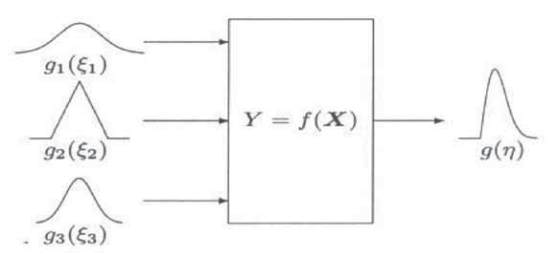
The figure 2 show an illustration of the concept of
propagation of distribution.
The model input quantities are X=(X1,X2,X3)T.
The probability density function , for Xi,i=1,2,3, are
Gaussian, triangular and Gaussian respectively.
The probability density function g(η) for the value of the
output quantity Y is indicated as being asymmetric, as
can arise for non linear models. An asymmetric output
PDF can also arise when the PDF for the values of input
quantities are asymmetric.
Approaches to uncertainty estimation
The ISO / IEC 17025 “General requirements for
competence of testing and calibration laboratories” in its
paragraphed dealing with uncertainty of measurement ( §
5.4.6) referred at the same level the ISO 5725 “Accuracy
(trueness and precision) of measurement methods and
results” and the GUM. So it seems important
for testing laboratory to develop approaches
consistent with the concept and recommendations
of the GUM but using others tools than the
procedure of chapter 8.
The paragraph 5.4.6.2 of ISO / IEC 17025
justifies entirely these new approaches : “Testing
laboratories shall have and shall apply procedures
for estimating uncertainty of measurement. In
certain cases the nature of the test method may
preclude rigorous, metrologically and statistically
valid, calculation of uncertainty of measurement.
In these cases the laboratory shall at least attempt
to identify all the components of uncertainty
and make a reasonable estimation of the uncertainty.
Reasonable estimation shall be based on knowledge of
the performance of the method and on the measurement
scope and shall make use of, previous experience and
validation data, for example”.
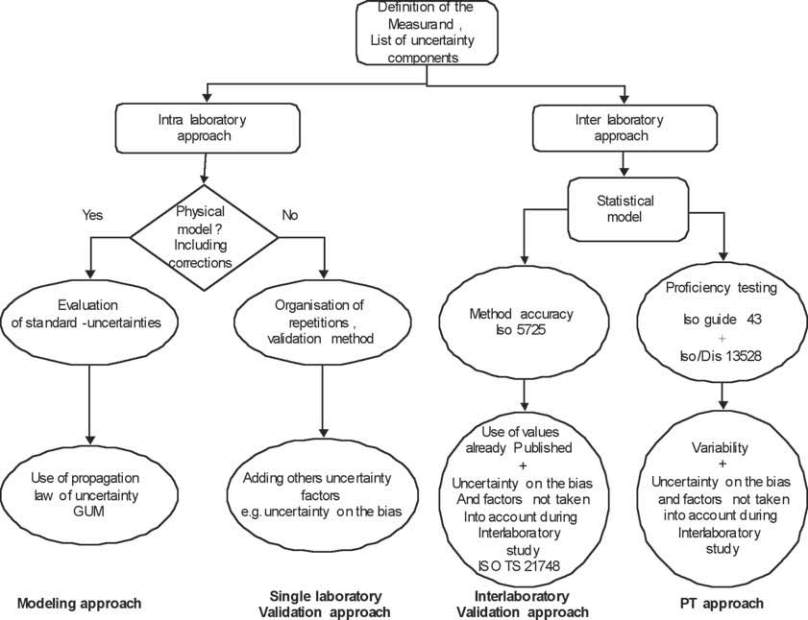
Road map of the different approaches
The figure 3 below shows a road map for uncertainty
evaluation.
Fig. 2: Illustration of the propagation of distributions
Fig. 3 : Typology of uncertainty evaluation methods
The approaches for measurement uncertainties evaluation