Version HTML de base
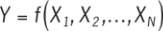
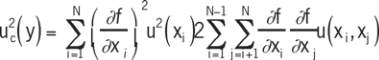
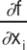
6
“Uncertainty-noise” Le Mans
Acoustique
&
Techniques n° 40
Three levels in the GUM can be identified:
- Basic concepts
- Recommendations
- Evaluation procedure
Consistency requires to approve the basic concept and
to follow recommendations. The procedure proposed in
the GUM (see chapter 8 of GUM: Summary of procedure
for evaluating and expressing uncertainty) is one of the
practical approaches for evaluating uncertainty but different
others approaches, all fully compliant with the GUM will
be presented in this document. In some circumstances
for example when it is impractical to identify all major
individual measurement uncertainty contributions, only
methods based on repeatability, reproducibility and
trueness estimate could be used.
Basic concepts of the GUM
The basic concepts in uncertainty evaluation are:
- The knowledge about any quantity that influence the
measurand is in principle incomplete and can be expressed
by a probability density function (PDF) for the values
attributable to the quantity base on that knowledge.
- The expectation value of that PDF is taken as the best
estimate of the value of the quantity.
- The standard deviation of that PDF is taken as the
standard uncertainty associated with that estimate.
The PDF is based on knowledge about a quantity that may
be inferred from.
- Repeated measurement: type A evaluation
- Scientific judgement based on all the available
information on the possible variability of the quantity: type
B evaluation
Recommendations
The GUM provides the following recommendations:
A model formulated to account for the interrelation of the
input quantities that influence the measurand.
This is certainly the most important aspect of the GUM, we
need to establish a relationship between the measurand
Y and N others quantities X
1
, X
2
,…, X
N
(input quantities)
through a function f:
where X
1
, X
2
,…, X
N
are all the relevant information used
to calculate the measuring result. Since this is generally
the most difficult part of the evaluation, the use of a
cause-effect relationship linking the input quantities to the
measurand is recommended. Correction included in the
model to account for systematic effects; such corrections
are essential for achieving traceability to stated references
(e.g. CRMs, reference measurement procedure, SI units).
Measurement result reports which indicate the value and
a quantitative indication of the quality of that result (the
uncertainty).
The provision of an interval about the measurement result
that may be encompass a large fraction of the values that
could be reasonably attributed to the measurand.
Procedure for uncertainty evaluation
People have often reduced the GUM to the procedure
summarized in the Chapter 8 of this document. The
following steps are proposed in the procedure.
- Derivation of the model of the measurement (the most
difficult task). The provision of probability density function
(PDFs) for the input quantities to the model, given
information about these quantities.
- In many case in practice, it is necessary to specify only
the expectation value and standard deviation of each PDF.
i.e. the best estimate of each quantity and the standard
uncertainty associated with that estimate.
- Propagation of uncertainty. The basic procedure (the law
of propagation of uncertainty) can be applied to linear or
linearized models, but subject to some restrictions.
This law, called propagation law of uncertainty is based on
a first order Taylor series expansion where,
u
c
2
(y) is the variance on the measuring result
is the partial derivative
u(x
i
,x
j
) is the covariance between x
i
and x
j
- Stating the complete result of a measurement by
providing the best estimate of the value of the measurand,
the combined standard uncertainty associated with that
estimate and an expanded uncertainty.
Some evolutions will appear soon, a supplement 1 to the
GUM [2] will develop advices concerning the numerical
methods for the propagation of distribution.
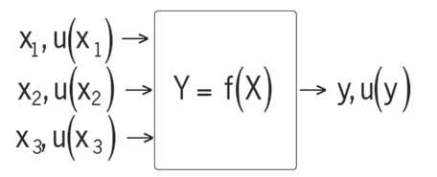
In the procedure, presented in the GUM, it is proposed to
the propagation law of uncertainty. The model has mutually
independent input quantities X=(X
1
,X
2
,X
3
)
T
whose value is
estimated by x
i
with associated standard uncertainty u(x
i
).
The value of the output quantity Y is estimated by y, with
associated standard uncertainty u(y).
Fig. 1 : Illustration of the law of propagation of uncertainty
The approaches for measurement uncertainties evaluation

