Version HTML de base
32
“Uncertainty-noise” Le Mans
Acoustique
&
Techniques n° 40
Statistical Energy Analysis
FEM (or BEM) techniques are usually effective for ‘low’
frequency evaluations. This is mainly due to the need for mesh
refinements as frequency increases. The related model size
(number of displacement and pressure degrees of freedom)
induced practical limitations that are, more andmore, overcome
by advanced solvers exploiting parallel architectures and
powerful processors. This recent trends allows for a significant
extension of frequency ranges where FEM techniques can be
applied. Such extension calls however for appropriate post-
processing techniques: local indicators are not meaningful
in such a context since they are strongly spatially variable
and too sensitive to model parameters. Global indicators
(spatially and/or frequency averaged) are requested and
can effectively be produced starting from extended modal
representations of complex vibro-acoustic systems [17].
Such an approach is also the basis for developing automatic
partitioning techniques [18,19,20] supporting the application
of SEA techniques. Additionally such advanced FE models can
support the evaluation of coupling loss factors and a more
precise evaluation of the injected power related to complex
random excitations (turbulent boundary layer for instance).
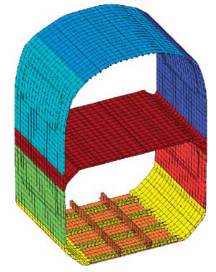
An example of energetic post-processing on a train structure
is provided in Fig. 4.
Conclusions
Vibro-acoustic simulations are generally affected by several
uncertainty sources appearing at different stages of the design
process. In the early modeling stage, a continuous model is set
up in simplification of a real physical behavior. The parameters of
this model are, inmost circumstances, not known with certainty.
In a vibro-acoustic context, the response variabilitymainly results
from a significant uncertainty in the structure characterization
(uncertain geometric configuration) and in the excitation model
(diffuse field and TBL). If sufficient information is available, a
probabilistic behavior for these unknown parameters can be
used (random variables or random processes) and appropriate
solution technique can be used. For low-frequency analysis,
the stochastic FEM provides efficient modal strategies that
enable the computation of the first and second-order response
statistics. Alternatively, fuzzy techniques can handle design
variables for which the probabilistic model is not suitable. As the
modal density increases, the response uncertainty is such that
the vibro-acoustic response should be investigated in terms of
spatial and/or frequency-averaged quantities. The resort to SEA
techniques can be secured by post-processingmodal FE-based
results in order to automatically build an SEA model.
Bibliography
[1] H.G. Matthies, Brenner C.E., Bucher C.G. and Guedes Soares C., Uncertainties
in probabilistic numerical analysis of structures and solids – stochastic finite
elements. Structural Safety, 19 (3), p. 283-336, 1997
[2] B. Van den Nieuwenhof – Stochastic finite elements for elastodynamics:
random field and shape uncertainty modelling using direct and modal
perturbation-based approaches. PhD thesis, Université catholique de Louvain,
2003
[3] J.F. Allard – Propagation of sound in porous media: modelling sound
absorbing materials. Elsevier Applied Science, 1993
[4] C. Soize – A nonparametric model of random uncertainties for reduced matrix
models in structural dynamics. Prob. Eng. Mech., 15, p. 277-294, 2000
[5] J.F. Durand, L. Gagliardini and C. Soize – Nonparametric modeling of the
variability of vehicle vibroacoustic behavior. SAE Conference, Paper 05NVC181,
2005
[6] G.I. Schuëller – A state of the art report on computational stochastic
mechanics : IASSAR report on Computational Stochastic Mechanics. Prob. Eng.
Mech., 12, p. 197-321, 1997
[7] B. Sudret and A. Der Kiureghian – Stochastic finite elements methods and
reliability analysis : a state-of-the-art report. Tech. Report UCB-SEMM-2000-08,
Berkeley, 2000
[8] M. Kleiber and T.D. Hien – The stochastic finite element method : basic
perturbation technique and computer implementation. Wiley & Sons, 1992
[9] R.G. Ghanem and P.D. Spanos – Stochastic finite elements : a spectral
approach. Springer-Verlag, 1991
[10] M. Papadrakakis and A. Kotsopoulos – Parallel solution methods for
stochastic finite element analysis using Monte-Carlo simulation. Comput. Meth.
Appl. Mech. Engrg., 168, p. 305-320, 1999
[11] R.G. Ghanem and R.M. Kruger – Numerical solution of spectral stochastic
finite element systems. Comput. Meth. Appl. Mech. Engrg., 129, p. 289-303,
1996
[12] B. Van den Nieuwenhof, J.-P. Coyette – Modal approaches for the stochastic
finite element analysis of structures with material and geometric uncertainties.
Comput. Methods Appl. Mech. Engrg., 192, p. 3705-3729, 2003
[13] E. Vanmarcke, Random fields : analysis and synthesis. MIT Press, 1993
[14] J.L. Guyader and E. Rebillard – Hypersensitivity of vibroacoustics behaviour
of plate lattices. Proc. Internoise 96, p. 1373-1376, 1996
[15] D. Moens and D. Vandepitte – Fuzzy finite element method for frequency
response function analysis of uncertain structures. AIAA J., 40 (1), p. 126-136,
2002
[16] B. Van den Nieuwenhof and J.P. Coyette – Time harmonic dynamic analysis
of uncertain structures using Fuzzy Finite Element techniques, Tech. Report
2003-01, Louvain-la-Neuve, 2003
[17] ACTRAN/HF User’s manual, Free Field Technologies S.A., Louvain-la-Neuve,
2005 (see http://www.fft.be)
[18] B.Mace and P.J. Shorter – Energy flow models from finite element analysis.
J. Sound Vibr., 233 (3), p. 369-389, 2000
[19] N.Totaro – Caractérisation de sources aérodynamiques et sous-structuration
pour la méthode SEA. PhD Thesis, Institut National des Sciences Appliquées de
Lyon, 2004
[20] L. Maxit and J.L. Guyader – Estimation of SEA coupling loss factors using a
dual formulation and FEM modal information, part I : Theory. J. Sound Vibr., 239
(5), p. 907-930, 2001
■
Fig 4 : Optimal SEA subsystems for a train structure model

