Version HTML de base
“Uncertainty-noise” Le Mans
31
Acoustique
&
Techniques n° 40
random variables NKV giving a good variance representation
of the field.
Secondly, considering the possibility of the development of a
compensation effect (depending on response characteristics
and random field parameters), this theoretical number can
be reduced.
Thirdly, the discretisation mesh is selected in such a way
that it is compatible with the discretisation technique (a finer
mesh should be selected for the midpoint discretisation than
for the Karhunen-Loeve expansion technique). This mesh
should allow for a good representation of the random field
(sufficient number of subdivisions per correlation length and
per eigenfunction wavelength). If we note by NEL or NND the
number of elements and nodes of this mesh, the truncation
ratio r is finally selected in such a way that r x NND=NKV or
r x NEL=NKV for the Karhunen-Loeve expansion or midpoint
discretisation, respectively.
Shape uncertainty
Most SFEM applications in the literature involve uncertain
parameters of material or mechanical nature and rarely of
geometrical nature. Random shape variables result in uncertain
domains and boundaries, which complicate the stochastic
analysis. Generally, applications aimed at characterizing the
response variability resulting from a geometric uncertainty
source are based on models allowing particular kinematic
assumptions. In such cases, the treatment of the geometric
variables by the same means as the material parameters (for
instance the cross-section of a beam element or the thickness
of a plane stress model) is possible. Only a few applications
really handle the shape randomness. However, geometric
uncertainties can be found in a wide range of mechanical
applications and should consequently be addressed in a
general framework.
The perturbation SFEM, used in conjunction with the shape
design sensitivity theory, offers a possibility to develop an
efficient technique for handling geometric uncertainties [12].
As an example, Fig. 2 shows the variability of the vertical
displacement field for a plate having a random flatness default.
Due to the apparition of stiffening membrane effects, the
displacement field exhibits an hypersensitive behavior w.r.t.
the low non-planearities [14].
This effect should be accounted for in explaining the scatter in
the vibro-acoustic behavior of industrially identical structures
(see Fig. 2).
Fuzzy Finite Elements
Fuzzy logic and fuzzy arithmetics have also been applied to the
field of finite element analysis. In fact, not all uncertainties are
objectively quantifiable, especially those based on incomplete
information, and can therefore not be handled satisfactorily
in the probability theory. In fuzzy FE analysis, each uncertain
property and each response value is represented by a fuzzy
number, defined by its membership function. Fuzzy numbers
are then discretized by performing cuts at given degrees of
membership, which reduces the analysis to the solution of
interval arithmetic problems.
The use of interval arithmetics however restricts the tractability
of the method to small systems (the problem inversion being
computationally tedious) and, if not carefully controlled, leads
to an artificial augmentation of the interval sizes. Circumventing
this spurious behavior, the combinatorial approach (vertex
method), consists in considering all possible combinations for
the upper and lower bounds of the design parameter intervals.
Specific modal-based methods for the structural dynamics
in the frequency domain have been proposed by Moens and
Vandepitte [15].
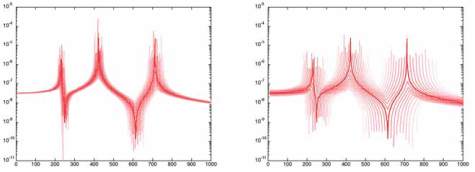
Recent results [16] tend to show that adding sensitivity-based
information in the construction of the fuzzy response enables
to achieve better efficiency in the numerical procedure. As an
example, Fig. 3 shows, for two uncertainty levels, the fuzzy
frequency response function for a displacement dof in an
articulated truss structure.
Fig. 3 : Articulated truss structure : fuzzy FRF of the displacement field (all parameters having 3% (left) or 10% (right) of variability)

