Version HTML de base
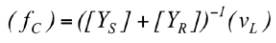
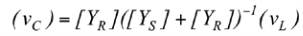
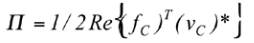
41
Spécial « Vibrations dans les bâtiments »
Outils de modélisation de la propagation couplée sol-structure
Du fait des fréquences ferroviaires basses (habituellement
la partie significative du spectre est inférieure à 150 Hz)
le système Source-Récepteur illustré sur la figure 2 peut
être approché en 2D par deux points de contact entre les
parties inférieures et supérieures avec 3 degrés de liberté
par contact (composantes horizontale (en x) et verticale
des vitesses, ainsi que la rotation autour de z).
La Source est caractérisée par :
- un vecteur vitesse libre (
vƒ
) ayant 6 composantes
(2 points de contact) et
- une matrice 6x6 [
Y
S
] de mobilité de la source incluant les
termes de mobilité de transfert d’un contact à l’autre (la mobi-
lité est le rapport entre la vitesse et la force appliquée).
Le Récepteur est également caractérisé par une matrice
de mobilité [
Y
R
].
Les forces de contact (
ƒ
C
) et les vitesses de contact (
v
C
)
ainsi que la puissance transférée entre la source et le
récepteur peuvent être estimées à partir des quantités
définies précédemment à l’aide des expressions :
(2)
(3)
(4)
Toutes les quantités employées dans les équations (2) à (4)
sont complexes et peuvent être exprimées en termes d’une
amplitude et d’une phase. Il convient de remarquer que les
forces de contact, les vitesses et la puissance peuvent être
calculées séparément pour chaque point de contact et pour
chaque type d’onde (longitudinale et flexion en combinant
les composantes horizontales et angulaires).
Les caractéristiques de la Source (vitesse libre et mobi-
lités des fondations) sont estimées par calcul avec les
modèles FEM/BEM décrits précédemment ; les mobili-
tés du Récepteur (le bâtiment déconnecté de ses fonda-
tions) sont estimées par le modèle purement structural
choisi pour le bâtiment.
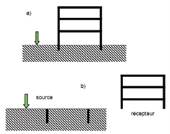
Fig. 2 : Séparation d’un problème (a) en deux
parties (b) : source/récepteur
Une description plus complète de cette approche est
donnée en [4].
Cette approche permet l’emploi de deux logiciels sépa-
rés pour la partie sol/fondation et la partie superstruc-
ture. Les équations (1) - (3) sont généralisables au 3D.
Une approche intermédiaire entre 2D et 3D consiste à
utiliser un calcul 2,5D pour les sols et les fondations qui
permet d’accéder à tous les degrés de liberté néces-
saire au calcul de l’interaction 3D en supposant toute-
fois que la fondation est infinie (les fondations de type
pieux sont alors exclues).
Applications
Validation expérimentale ferroviaire
Une étude de la propagation des vibrations ferroviai -
res vers un bâtiment voisin a été menée à partir d’une
campagne de mesures effectuée dans le cadre du projet
PREDIT Vibsolfret [12], au cours de laquelle l’atténuation
des ondes de surface en fonction de l’éloignement aux
voies a permis une confrontation avec le calcul BEM.
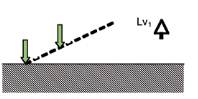
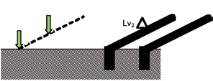
Les calculs ont montré que seul le modèle 2,5D permet
de retrouver les bonnes atténuations (configuration de la
figure 3a). Le modèle 2,5D est plus proche de la réalité
puisqu’il permet de définir une ligne de sources inco-
hérentes alors que le modèle 2D assimile les sources
à des lignes infinies cohérentes. Des mesures vibratoi -
res au sol en champ libre permettent alors de calibrer
le modèle.
Fig. 3 a et b : Configuration 2D
1
/
2
de la Source (sol + fondations)
Les calculs 2,5D, bien que moins coûteux que les calculs
3D (maillage d’une section 2D au lieu du maillage complet
3D) demeurent bien plus gourmands en temps CPU que
le calcul 2D. C’est pourquoi une fonction de recalage
entre 2D et 2,5D a été définie comme suit.
Le modèle BEM a été appliqué en 2D puis en 2,5D au calcul
de la perte par insertion d’une fondation IL=LV(avec) -
LV(sans fondation). Cette fonction IL est employée pour
construire le terme de recalage H=IL(2D) - IL(2,5D).
a
b

