Version HTML de base

13
Spécial « Vibrations dans les bâtiments »
Les vibrations causées par le trafic ferroviaire de surface
- au niveau du bâtiment (étape 6 de la figure 2), son compor-
tement vibratoire piloté par l’épaisseur et la nature de ses
parois/planchers/fondations.
Face à un tel degré de complexité, l’approche numérique
paraît être parfaitement adaptée pour optimiser des solu-
tions de réduction.
Modélisations numériques
Des approches numériques ont été développées pour
prédire et mieux appréhender les vibrations transmises
par le sol. Ces approches sont basées sur une modéli-
sation par éléments de frontières du demi-espace repré-
sentant le sol.
Ces modèles ont été adaptés pour le cas ferroviaire :
- à partir de modèle BEM 3D (boundary element model/
éléments de frontière) pour modéliser la propagation des
ondes dans le sol, la périodicité longitudinale de la voie
permet de passer à des modèles dits 2,5D. En effet, en
supposant le système invariant dans la direction longitudi-
nale de la voie y, la propagation des ondes dans le système
est estimée par une approche BEM pour une tranche de la
voie, pour chaque nombre d’onde k
y
et la réponse totale
est recomposée par transformée de Fourier inverse en
espace, en sommant sur les k
y
;
- la rugosité est décomposée sur la base des k
y
;
- la voie est représentée par un ensemble de systèmes
masses/ressorts/amortisseurs couplé au sol. Une modé-
lisation par éléments finis de la plate-forme (couches d’as-
sise de la voie) peut aussi être envisagée ;
- le comportement vibratoire du bâtiment peut être pris en
compte par un modèle éléments finis du bâtiment, couplé
au sol via ses fondations.
Ces modèles permettent d’estimer les vibrations dues au
trafic ferroviaire. Pour obtenir une modélisation pertinente,
il faut caractériser un grand nombre de paramètres pilo-
tant les réponses dynamiques des différents systèmes :
voie-sol-bâtiment.
Fig. 3 : Mesures sur site : à gauche, charge impulsionnelle par
impact de marteau pour une caractérisation de sol par
méthode MASW, au centre, distribution d’accéléromètres
en champ libre pour une caractérisation de sol par
méthode MASW, à droite, charge impulsionnelle sur
le rail pour une mesure de réceptance de voie
Ainsi, pour déterminer le comportement du sol, les vites-
ses de propagation des ondes dans le sol sont mesu-
rées par méthode MASW (figure 3, photographies de
gauche et du centre). Le sol est excité via une charge
impulsionnelle (chocs de marteau par exemple) et les
niveaux accélérométriques sont mesurés à différentes
distances du point d’impact.
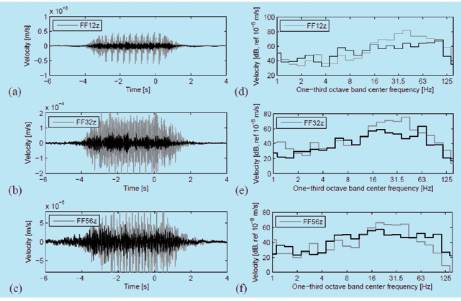
Fig. 4 : Comparaison de signaux temporels (a), (b) et (c), et de spectres 1/3 d’octave (d), (e) et (f), mesurés (en noir) ou simulés (en
gris) en champ libre, à différentes distances de la voie (12 m, 32 m et 56 m respectivement), passage d’un TGVA à 200 km/h

