Version HTML de base

39
Caractérisation dynamique des matériaux et réduction des nuisances vibroacoustiques : l’apport des vibrations. Partie 1
Les céramiques peuvent être en contact (mode direct)
avec le matériau à caractériser ou couplées par un
fluide (mode immergé). Ce dernier permet de faire
varier l ’angle d’incidence du faisceau d’ultrasons par
rapport à la face de l ’échantillon et ainsi de détermi -
ner les caractéristiques de matériaux anisotropes,
figure 24.
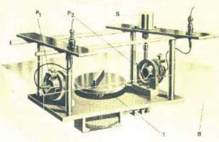
Fig. 24: Cuve de mesure US. D’après B.E Read &
G.D Dean The determination of dynamic
properties of polymers and composites
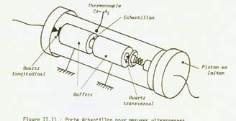
Les mesures au contact permet tent de caractéri -
ser les matériaux homogènes. Un exemple est four-
nit f igure 25. L’échanti l lon de petite tai l le est placé
entre deux buf fers métal l iques jouant le rôle de l igne
à retard.
Les générateurs piézoélectriques (5 MHz) d’ondes longi-
tudinales et transversales sont mis en pression de part et
d’autre des buffers. L’ensemble est positionné dans une
enveloppe thermostatée.
Fig. 25 : Dispositif de mesure US. D’après M .Salvia Thése :
Propriétés dynamiques des propergols solides
Ce dispositif a permis la mesure simultanée des vites-
ses de propagation longitudinale et transversale en
fonction de la température en dessous de la tempéra-
ture de transition Tg (voisine de -80°C). En effet autour
et au-dessus de Tg l ’absorption dans le matériau est
telle que l ’écho disparaî t. Les résultats de la mesure
de la vitesse Transversale et du calcul du module de
cisaillement pour une matrice Polybutadiène à dif fé-
rents taux de charges sont regroupées figures 26.
Fig. 26 : Module de cisaillement vs Vt pour différents
taux de charge. D’après : idem 25
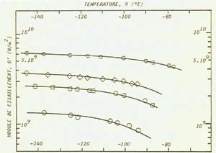
A partir des résultats précédents et de la mesure de
la vitesse transversale Vt, le coefficient de Poisson est
calculé, figure 27.
Fig. 27 : Calcul dU coefficient de Poisson
Sur le plateau vitreux, le coefficient de Poisson varie entre
0,25 et 0,30 respectivement pour la matrice chargée et la
matrice pure. Autour de Tg le coefficient augmente rapi-
dement pour atteindre une valeur voisine de 0,5.
Il est remarquable de noter que cette technique est unique
pour la caractérisation dynamique complète d’un solide.
En effet la mesure simultanée des vitesses longitudinale et
transversale suffit pour remonter au module de cisaillement
G et au module de plaque L =
λ
+2G, connaissant la masse
volumique. À partir de ces grandeurs il est alors possible
de calculer : le module d’Young E, le module de compres-
sibilité volumique B et le coefficient de Poisson
ν
.
La gamme de fréquence accessible se situe entre quel-
ques centaines de kHz et plusieurs MHz. Dans ce domaine
de fréquence les amplitudes des ondes sont très faibles
et par conséquent les taux de déformation appliqués à
l’échantillon restent très faibles. Il faut de plus que les
dimensions latérales de l’échantillon soient très supé-
rieures à la longueur d’onde de l’excitation de manière à
se placer dans un mode de propagation longitudinale en
onde plane. Les mesures en température sont possibles
et sont limitées par la tenue des interfaces et de la tempé-
rature de Curie des éléments piézoélectriques.

