Version HTML de base


32
Caractérisation dynamique des matériaux et réduction des nuisances vibroacoustiques : l’apport des vibrations. Partie 1
ment périodique), au sein d’un système, capable de durer
indéfiniment sans apport extérieur d’énergie ou de matière,
ni transformation irréversible du système. Dans le monde
réel rien n’est parfait et il y a dissipation d’énergie à toutes
les échelles; tout d’abord au niveau des matériaux eux-
mêmes, soit au niveau des assemblages, soit au niveau
des interactions (couplage) entre la structure vibrante et
le milieu environnant (air ou eau).
Il existe plusieurs mécanismes d’amortissement interne:
l’amortissement intrinsèque (frottement intérieur) et l’hys-
térésis. Pour les premiers, on observe une constante de
temps spécifique : l’énergie est dégradée de manière
privilégiée autour d’une fréquence caractéristique. Quant
aux mécanismes d’hystérésis, ce sont des processus qui
dépendent du temps; ils absorbent de l’énergie à toutes
les fréquences.
En fait, dans toute pièce de forme déterminée soumise à des
sollicitations cycliques, deux phénomènes coexistent :
- un phénomène intéressant les mécaniciens qui cher-
chent à déterminer la fréquence propre de la vibration en
connaissant le module d’élasticité (Module d’Young en Pa)
et la masse volumique (ƒ en kg/m
3
) du matériau,
- un phénomène intéressant les physiciens qui cherchent à
déterminer la réponse et les contraintes dans le matériau.
Si par exemple on frappe sur plusieurs barreaux de même
géométrie dont l’un est en acier et les autres en fontes, le
son émis n’est pas le même (premier phénomène) et la durée
d’émission n’est pas la même (deuxième phénomène). La
diminution d’amplitude du phénomène est plus rapide pour
les fontes que pour l’acier, comme l’illustre la figure 3.
Fig. 3 : Atténuation des vibrations de l’acier
et diverses fontes (unités arbitraires)
L’amplitude de la déformation cyclique est maximale lors-
que la fréquence d’excitation est égale à la fréquence
propre, on parle alors de résonance. En l’absence d’amor-
tissement, la réponse serait infinie.
En réalité il n’en est rien, car si on trace un diagramme
(contrainte appliquée sur déformation subie), on constate
que sur un cycle complet on obtient une courbe fermée,
dont l’aire représente l’énergie dissipée dans le matériau
au cours d’un cycle (figure 4).
Fig. 4 : Cycle effort-déformation d’une éprouvette de fonte
grise en vibration forcée (unités arbitraires)
Le facteur d’amortissement est une mesure du rapport
de l’énergie dissipée par amortissement à l’énergie élas-
tique conservée puis restituée durant un cycle de défor-
mation sinusoïdale.
Le facteur de perte (loss factor) en traction est égal à :
η
: Facteur de perte (sans unité ou exprimé en %)
ω
: Fréquence angulaire en rd/s
T : Température en °C
δ
: Angle de déphasage en ° entre la contrainte appliquée
au matériau et sa déformation
E’, E’’, Ec et Ed représentent respectivement le module de
conservation d’énergie (partie réelle du module d’Young
complexe) exprimé en Pa, le module de perte d’énergie (partie
imaginaire du module d’Young complexe) exprimé en Pa,
l’énergie conservée et l’énergie dissipée par unité de volume
(J/m
3
) durant un cycle de déformation sinusoïdale.
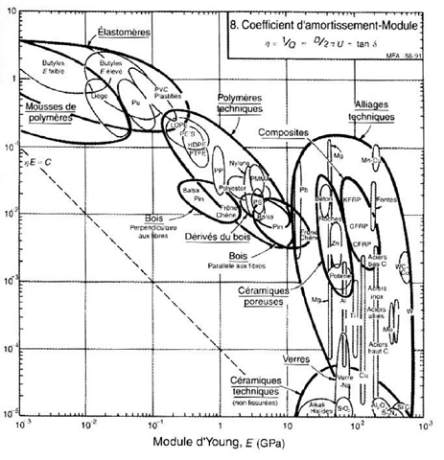
Fig.5 : Diagramme amortissement- module d’Young (D’après
M.F.Ashby-Choix des matériaux en conception mécanique

