Version HTML de base
Spécial “ 5es Assises sonore ”
7
Acoustique
&
Techniques n° 51
Variabilité spatio-temporelle et incertitudes des données d’entrée des modèles de prévision acoustique
fait apparaître un seul paramètre phénoménologique : la
résistance spécifique au passage de l’air «
σ
». On peut
éventuellement lui ajouter un «effet d’épaisseur» à travers
l’introduction du paramètre d’épaisseur «e» [19].
La détermination des valeurs de
σ
et e implique donc un post-
traitement. Aussi, l'opérateur doit se donner des critères de
calage, le principal critère étant le respect de la position et
de l’amplitude du premier creux très marqué (Figure 2(b)). Les
opérations de calage sur les mesures de suivi spatial ("Méthode
LCPC") ont été effectuées par 3 techniciens, et celles des
mesures en continu ("Méthode EDF") par 2 techniciens. Ainsi
le résultat de la moyenne sur 2 ou 3 opérateurs a permis,
dans une certaine mesure, de réduire les incertitudes liées
à l’opérateur, i.e. à l'interprétation subjective du calage. Par
ailleurs, pour une meilleure comparaison des 2 méthodes de
mesure, les valeurs obtenues par la méthode LCPC sont en
fait les moyennes des valeurs des 3 points de mesure pris
autour du point de mesure en continu (méthode EDF).
On limite ainsi les écarts dus à la surface d’étude, qui n’est
pas exactement la même avec les 2 méthodes. Finalement,
les incertitudes proviennent essentiellement des conditions
expérimentales et du traitement qui en est réalisé par la suite.
Considérant une plage de valeurs pour un sol du type herbeux
comme celui-ci, cette incertitude expérimentale de traitement
sur
σ
est ainsi estimée à +/- 20 kNsm
-4
(cgs). Les principes
d’acquisition et de traitement de ces données expérimentales
sont reportés en Figure 2.
La suite de cette analyse se focalise sur les valeurs d’un
seul paramètre :
σ
. En effet, les résultats montrent une faible
variation de l’épaisseur autour de 2 cm. Ceci constitue une
approximation, faite pour conduire cette première étude de
sensibilité. Dans de futurs travaux, il serait intéressant de
considérer le couple (
σ
,e) plutôt que le seul paramètre
σ
, voire
davantage de paramètres phénoménologiques en utilisant
d’autres modèles d’impédance [20].
Influence de la méthodologie de mesure d’impédance
de sol sur les niveaux sonores
Dans un premier temps, nous comparons l’influence des
différences entre les 2 méthodes d’évaluation du paramètre
σ
au même «point» (plus rigoureusement, il faudrait plutôt
parler de «zone d’étude»). Les évolutions temporelles
correspondantes sur toute la période de la campagne
expérimentale sont présentées sur la Figure 3(a). Sur les 2
courbes, nous pouvons observer qu’une tendance générale
apparaît clairement.
À partir du 8 juin, la résistance spécifique au passage de l’air
est plus élevée et semble subir de fortes variations. Ensuite,
un pic important apparaît autour du 14 juin, date à partir de
laquelle
σ
décroît fortement, puis plus doucement jusqu'à
mi-juillet. Enfin, jusqu'à fin août, elle stagne dans des valeurs
plus faibles et quasi constantes. Cette tendance générale
est bien commune aux 2 courbes. Elle peut s’expliquer par
l’évolution temporelle des caractéristiques d’humidité de
surface (pluie/assèchement - voir Section suivante).
Par contre, il existe un décalage quasi-permanent de l’ordre
de 50 kNsm
-4
entre les deux méthodes. Cet écart dépend
donc de la méthode de mesure et peut être considéré
comme une cause supplémentaire d’incertitude de mesure du
paramètre
σ
puisque les deux méthodes de caractérisation
sont - a priori - valides. Cette translation doit être rapprochée
des différences de géométrie, d’acquisition et de traitement
entre les deux méthodes.
Pour illustrer l’influence de ce décalage sur le calcul de
niveaux sonores, la Figure 3(b) donne l’évolution des
niveaux sonores relatifs au champ libre à 1 kHz en fonction
de la distance à la source à 2 m de hauteur. Les variations
d’amplitude autour de cette fréquence de 1 kHz sont assez
représentatives des variations du niveau global A.
La configuration étudiée est typique d’une situation de
bruit routier : source très proche du sol (5 cm) et rupture
d’impédance à 5 m de la source (sol réfléchissant/impédant).
Le modèle utilisé est basé sur la résolution de l’équation de
Helmholtz (approximée par l’équation parabolique : PE) par
la méthode «split-step Padé» [16], en utilisant le modèle de
sol de Delany & Bazley [18] et un profil vertical de célérité du
type «log-lin» (Conditions favorables : Alog = 1 et Blin = 0,12,
en accord avec [21]).
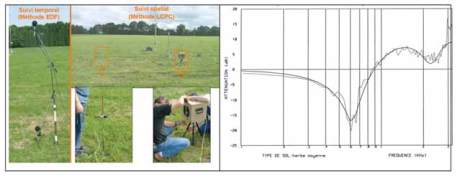
Fig. 2 : Campagne expérimentale «Lannemezan 2005» - (a) principe d’acquisition expérimentale et (b)
de post- traitement pour la détermination de la résistance spécifique au passage de l’air
σ
«Lannemezan 2005» experimental campaign - Principle of (a) experimental data acquisition
and (b) data post-processing for the determination of the specific air flow resistivity
σ

