Version HTML de base
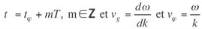
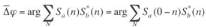
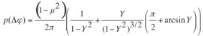
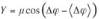
34
Spécial “ Acoustique sous-marine ”
Acoustique
&
Techniques n° 48
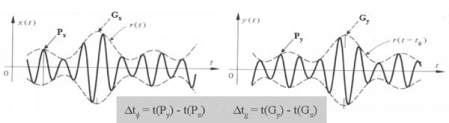
La figure 8 présente deux signaux dont l’un correspond au
point d’émission et le deuxième au point de réception. Dans
ce cas, les deux temps sont différents même à une période
près : l’équation (8) n’est plus vérifiée.
(8)
Avec
ω
, pulsation et k, vecteur d’onde.
Physiquement, le facteur m représente une notion de retard
en relation avec la vitesse de groupe vg : il s’agit d’une
mesure de différence de temps de propagation, entre deux
capteurs, d’une onde modulée par le relief. En revanche,
l’interférométrie utilise la phase du signal, phase qui est
directement en relation avec la vitesse de phase v
ϕ
. Si on
ne peut pas utiliser la relation (8), c’est-à-dire si les deux
vitesses diffèrent, il n’est plus possible de retrouver le retard
non ambigu. En fait, ces vitesses diffèrent dès que l’indice
du milieu dépend de la fréquence. Dans le milieu marin, en
première approximation, ce n’est pas le cas, cet indice est
essentiellement sensible à la pression, la température et
la salinité. On note nT, le retard grossier et t
ϕ
,, le retard
interférométrique ou retard fin.
Méthodes de lever d’ambiguïté [3]
Fondamentalement, les origines du facteur n et de la différence
de phase
Δϕ
sont radicalement différentes et les méthodes
d’estimation de ces deux quantités le sont aussi. Ainsi plusieurs
méthodes existent pour remonter au facteur n : la méthode
du Vernier, les méthodes haute résolution (comme Music),
l’intercorrélation des signaux ou encore, la formation de voie
et d’autres…
Interférogramme
À la différence de l’optique, l’effet interférométrique en sonar,
provient d’un calcul et non d’un phénomène d’interférence.
Cela présente à première vue des avantages car beaucoup
de traitements sont envisageables, en particulier tirer profit
de la flexibilité du calcul pour améliorer les qualités de
l’interférogramme. Le terme
*
b a
SS
est un terme souvent très
bruité (bruit de phase) et il est nécessaire d’avoir recours à une
approche multilook pour améliorer la qualité de l’estimation de
l’argument de ce dernier, c’est-à-dire utiliser plusieurs mesures,
plusieurs échantillons et un estimateur du type maximum de
vraisemblance ; celui-ci est donné par l’équation 0.
(9)
On voit sur cette équation que la quantité dont on extrait
l’argument en « multilook » n’est autre que l’intercorrélation
de deux signaux pour l’instant nul, et avec une fenêtre de
troncature de N points ; pour le cas du « monolook », cette
intercorrélation est réduite à un seul point. Concrètement, la
qualité de l’estimation augmente avec la longueur de la fenêtre
du multilook, or si les signaux utilisés sont à bande large et
qu’une compression d’impulsion est appliquée, la résolution
au sol est supérieure à celle d’un signal à bande étroite ; cela
signifie que pour une résolution au sol identique, l’estimation
de la phase interférométrique pour un signal bande étroite
(single-look) est bien moins bonne que celle d’un signal bande
large (multilook).
Notion de bruit [4] [5]
Le bruit interférométrique est l’élément dimensionnant
pour l’exploitation de la phase interférométrique et le lever
d’ambiguïté. Il existe deux types de bruit : le bruit extrinsèque
lié à des erreurs de mesures, et le bruit intrinsèque lié aux
phénomènes de décorrélation du signal. Ce dernier provient
de plusieurs phénomènes : la décorrélation angulaire, la
décorrélation spatiale, les trajets multiples et la présence
de bruit ambiant. Ceux-ci dégradent le coefficient de
corrélation.
Cette notion de coefficient de corrélation est fondamentale
car la statistique de la phase interférométrique pour des
signaux capteurs gaussiens (phase et quadrature) est définie
par deux paramètres : la valeur moyenne <
Δϕ
> de la phase
interférométrique et le coefficient de corrélation µ, qui est
bijectivement lié à la variance de la phase interférométrique,
comme indiqué par l’équation (10).
(10)
avec
et
μ
, le coefficient de
corrélation.
Plus le coefficient de corrélation µ est proche de 1, plus la
qualité du signal est importante.
Fig. 8 : Différences entre vitesse de groupe & vitesse de phase
Sonars cartographiques et interférométrie associée

