Version HTML de base
8
e
CFA - Tours 2006
21
Acoustique
&
Techniques n° 45
montre la dépendance de l’amplitude du spectre pour des
barreaux sains et dégradés.
La palette de couleur traduit l’amplitude de la
composante fréquentielle mesurée. La figure montre de
façon évidente la présence d’une abondante richesse
des harmoniques dans l’échantillon dégradé alors que
l’échantillon sain (linéaire) reste insensible à la variation
d’amplitude d’excitation V
1
. Cette augmentation drastique
est également visible sur la Figure 5b où l’amplitude des
termes d’intermodulation du premier et du second ordre
sont exprimés en fonction de l’amplitude du fondamental
f
1
, dans le cas intact et dégradé. Dans ce dernier cas,
la pente semble proche de l’unité pour f
1
+ f
2
, le terme
« somme » du premier ordre, et une pente entre 1 et 2,
pour 2f
1
+ f
2
., terme « somme » du second ordre. Des
résultats similaires ont été obtenus pour les termes
« différence » d’ordre 1 et 2.
Spectroscopie par propagation non linéaire d’ondes
acoustiques
Le troisième et dernier exemple est une illustration
de la méthode de Spectroscopie par propagation non
linéaire d’ondes (NWPS pour Nonlinear Wave Propagation
Spectroscopy [4-5]). Cette méthode consiste simplement
à quantifier, en fonction de l’amplitude du fondamental, le
niveau d’harmonique généré par une onde sinusoïdale se
propageant à travers l’échantillon. Ici, nous choisissons,
pour illustrer cette méthode, une application qui n’est pas
particulièrement associée à l’évaluation de la dégradation.
La méthode NWPS a été appliquée pour évaluer les étapes
des changements de la microstructure dans un béton au
cours du processus d’hydratation [22-24]. Pour ce faire,
un système intégré, comprenant un dispositif actif et
passif a été conçu. Ce système est élaboré à partir d’un
système d’émission acoustique (EA) d’une part, et d’un
dispositif de caractérisation de vitesse de pulse et de
génération d’harmonique lors de la propagation d’ondes
longitudinale (P) et transverses (S), d’autre part.
Les coefficients non linéaires sont obtenus par l’évaluation
des harmoniques A2 à la fréquence double et présents
dans un train d’ondes à 100 kHz (séquentiellement pour
les ondes S et P), en fonction de la réponse du fondamental
A
1
. Le coefficient de proportionnalité, que présente la loi
quadratique entre A
2
et A
1
permet d’accéder à la valeur
de la signature de la non-linéarité. La figure 6 illustre
l’évolution de cette valeur mesurée pendant trois jours, en
fonction du temps.
En observant le profil de température, la croissance
relativement lente est suivie par une brusque
augmentation, traduisant une accumulation interne de
chaleur provenant de réactions chimiques [23-24]. La
première réaction chimique démarre très tôt au cours
du processus, environ deux heures après la préparation
du béton, et l’augmentation atteint son maximum au bout
de 12 heures. C’est durant cette période que se forment
la plupart des agrégats entre les différents composés,
les premiers entre les plus petits et les derniers entre
les plus gros. Après avoir atteint le pic de température,
un processus de diffusion est à l’origine du remplissage
des pores de la matrice par les produits hydratants.
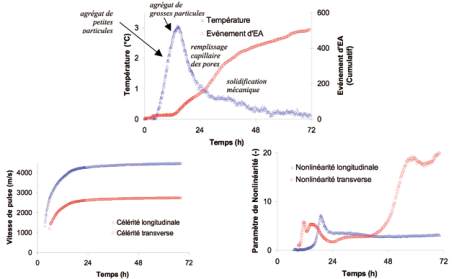
Fig. 6 : Évolution de la température, des événements cumulés d’Émission Acoustique,
de la vitesse des ondes S et P, et des coefficients de non-linéarité des ondes
S et P, au cours de la phase initiale du processus d’hydratation du béton
Détection et localisation de microdégradation de matériaux par spectroscopie d’ondes élastiques non linéaires

